Lattia- ja kattofunktio

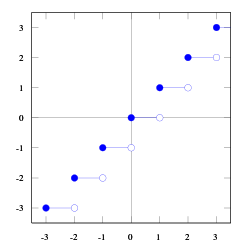
Lattia- ja kattofunktio ovat kaksi matematiikassa ja tietojenkäsittelytieteessä käytettävää funktiota, jotka muuntavat mielivaltaisen reaaliluvun kokonaisluvuksi.^[1]

Nimet "katto" (ceiling) ja "lattia" (floor) sekä vakiintuneet merkintätavat esitti ensimmäisenä Kenneth E. Iverson vuonna 1962. ^[2]

Lattiafunktio reaaliluvusta x, joka merkitään ${\displaystyle \lfloor x\rfloor }$ tai floor(x), palauttaa suurimman kokonaisluvun, joka on pienempi tai yhtäsuuri kuin x. Siis kaikille reaaliluvuille x pätee:

${\displaystyle \lfloor x\rfloor =\max \,\{n\in \mathbb {Z} \mid n\leq x\}.}$

Esimerkiksi floor(2.9) = 2, floor(−2) = −2 ja floor(−2.3) = −3.

Positiivisilla luvuilla x funktiota floor(x) voidaan kutsua myös x:n kokonaislukuosaksi. Funktio ${\displaystyle x-\lfloor x\rfloor }$ (myös x mod 1) on x:n desimaaliosa.

Kattofunktio, jota merkitään ${\displaystyle \lceil x\rceil }$ tai ceil(x), palauttaa pienimmän kokonaisluvun, joka on suurempi tai yhtäsuuri kuin x. Siis kaikille reaaliluvuille x pätee:

${\displaystyle \lceil x\rceil =\min\{n\in \mathbb {Z} \mid x\leq n\}}$

Esimerkiksi ceil(2,3) = 3, ceil(2) = 2 ja ceil(−2.3) = −2.

• Seuraava epäyhtälö on aina voimassa reaaliluvulle x :

${\displaystyle \lfloor x\rfloor \leq x<\lfloor x\rfloor +1}$

• Kun x ja n ovat positiivisia lukuja,

${\displaystyle \left\lfloor {\frac {n}{x}}\right\rfloor \geq {\frac {n}{x}}-{\frac {x-1}{x}}}$

• Lattiafunktio on idempotentti: ${\displaystyle \lfloor \lfloor x\rfloor \rfloor =\lfloor x\rfloor }$.
• Mille tahansa kokonaisluvulle k ja reaaliluvulle x,

${\displaystyle \lfloor {k+x}\rfloor =k+\lfloor x\rfloor }$

• Luvun x perinteinen pyöristäminen voidaan ilmaista tavalla: floor(x + 0,5)
• Lattiafunktio ei ole jatkuva, vaan puolijatkuva funktio. Vakiofunktiona sen derivaatta on nolla jokaisessa pisteessä jotka eivät ole kokonaislukuja.
• Jos x on reaaliluku ja n on kokonaisluku, pätee n ≤ x jos ja vain jos n ≤ floor(x).
• Reaalilukujen x, jotka eivät ole kokonaislukuja, lattiafunktio voidaan esittää Fourier-esityksenä:

${\displaystyle \lfloor x\rfloor =x-{\frac {1}{2}}+{\frac {1}{\pi }}\sum _{k=1}^{\infty }{\frac {\sin(2\pi kx)}{k}}}$

• Jos m ja n ovat keskenään jaottomia lukuja, niin

${\displaystyle \sum _{i=1}^{n-1}\lfloor im/n\rfloor =(m-1)(n-1)/2}$

• Jokaisen positiivisen kokonaisluvun k numeroiden määrä määritellään

${\displaystyle \lfloor \log _{10}(k)\rfloor +1}$

• Voidaan näyttää, että

${\displaystyle \lceil x\rceil =-\lfloor -x\rfloor }$

sekä

${\displaystyle x\leq \lceil x\rceil <x+1}$

• Jokaiselle kokonaisluvulle k pätee

${\displaystyle \lfloor k/2\rfloor +\lceil k/2\rceil =k}$