Varignonin lause (geometria)

Nykyään Varignonin lause (geometria) on erittäin tärkeä ja kiinnostava aihe laajalle ihmisjoukolle. Varignonin lause (geometria) on ollut viime vuosina lukuisten tutkimusten ja keskustelujen kohteena sen vaikutuksista yhteiskuntaan ja teknologiaan. Kun yleinen tietoisuus Varignonin lause (geometria):stä kasvaa, on tärkeää analysoida sen vaikutukset täysin ja ottaa huomioon mahdolliset pitkän aikavälin seuraukset. Tässä artikkelissa tutkimme Varignonin lause (geometria):een liittyviä eri puolia ja sen vaikutuksia jokapäiväisen elämän eri osa-alueisiin.

Nelikulmion sivujen keskipisteitä yhdistävät janat muodostavat nelikulmion (punainen), joka on aina suunnikas.

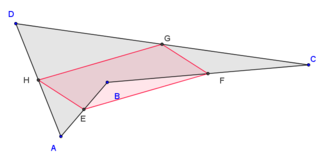
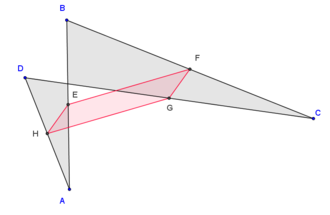
Varignonin lause on geometriassa Pierre Varignon vuonna 1831 todistama tulos, jonka mukaan nelikulmion sivujen keskipisteitä yhdistävät janat muodostavat aina suunnikkaan, oli nelikulmio minkä muotoinen tahansa. Suunnikasta kutsutaan siksi Varignonin suunnikkaaksi (engl. Varignon parallelogram).[1][2]

Ominaisuuksia

Varignonin suunnikkaan (vihreä) lävistäjät (siniset) ovat nelikulmion bimediaaneja. Punaiset janat ovat nelikulmion lävistäjät.
Sisäkkäiset Varignonin suunnikkaat pienenevät ja suppenevat pisteeseen, joka on nelikulmion keskipiste.
  • Varignonin suunnikkaan keskipiste löytyy sen lävistäjien leikkauspisteestä. Suunnikkaan lävistäjät puolittavat toisensa tässä keskipisteessä. Lävistäjät ovat alkuperäisen nelikulmion bimediaaneja.[3][4]
  • Varignonin suunnikkaan keskipiste ja nelikulmion kärkiin sijoitettujen samankokoisten massojen massakeskipiste sijaitsee samassa kohdassa.[3]
  • Varignonin suunnikkaan sivut ovat yhdensuuntaisia alkuperäisen nelikulmion lävistäjien kanssa.
  • Nelikulmion lävistäjien keskipisteitä yhdistävä jana kulkee Varignonin suunnikkaan keskipisteen kautta. Suunnikkaan keskipiste puolittaa myös tämän janan.[1]
  • Varignanin suunnikkaan pinta-ala on puolet alkuperäisen nelikulmion pinta-alasta.[1]
  • Varignanin suunnikkaan piiri on yhtä pitkä kuin alkuperäisen nelikulmion lävistäjien yhteispituus.[1]

Erikoistapauksia

Sekä yksinkertaisen että kompleksisen nelikulmion Varignonin suunnikkaalla on yleensä kahden pituiset sivut ja suuruiset kulmat. Silloin suunnikkaan lävistäjät ovat eri pituisia ja ne leikkaavat toisensa terävässä kulmassa.[3]

Kun nelikulmio on yleinen nelikulmio, puolisuunnikas tai suunnikas, on Varignonin suunnikas aina yleinen suunnikas. Kun nelikulmio on tasakylkinen puolisuunnikas tai suorakulmio, on Varignonin suunnikas neljäkäs. Vielä, kun nelikulmio on neljäkäs tai leija, on Varignonin suunnikas aina suorakulmio. Nelikulmion ollessa neliö, on myös Varignonin suunnikas neliö.[5]

Jos Varignonin suunnikkaan sisälle piirtää toisen Vargnonin suunnikkaan, on myös se suunnikas. Lisäämällä toistuvasti uusien Varignonin suunnikkaiden piirtämistä sisempien Varignonin suunnikkaiden sisälle, syntyy loputon jono pieneneviä suunnikkaita. Näiden suunnikkaiden kuvioiden jono suppenee yhteen pisteeseen, joka on nelikulmion keskipiste. Lukuun ottamatta ensimmäistä nelikulmiota, ovat jonon parilliset jäsenet yhdenmuotoisia keskenään, ja jonon muut kuviot ovat taas yhdenmuotoisia vain keskenään.[6]

Konveksi nelikulmio Konkaavi nelikulmio Rusettinelikulmio

Todistus

Lause voidaan todistaa homotetian avulla: Soveltamalla homotetiaa keskipisteitä yhdistävään janaan homotetiakeskuksena neliön kärkipisteet kertoimella 2 nähdään, että nelikulmion keskipisteitä yhdistävät janat kuvautuvat nelikulmion lävistäjiksi. Koska homotetia säilyttää janojen yhdensuuntaisuuden, on keskipisteitä yhdistävät vastakkaiset janat yhdensuuntaiset, eli nelikulmio on suunnikas.

Yleistys

Keskinen kolmio on vastaava tilanne kolmiolla. Jos merkitään monikulmion sivuille keskipisteet ja yhdistetään viereiset keskipisteet janoilla, saadaan muodostettua keskinen monikulmio mille monikulmiolle tahansa.[6][7]

Katso myös

Lähteet

Viitteet

  1. ↑ a b c d Weisstein, Eric W.: Varignon's Theorem (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
  2. ↑ Compendium Geometry: Varignon parallelogram
  3. ↑ a b c Weisstein, Eric W.: Varignon Parallelogram (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
  4. ↑ Weisstein, Eric W.: Bimedian (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
  5. ↑ Cource E: 7 th Chapter: Properties of 2-D figures, s.407 (Arkistoitu – Internet Archive), York Catholic
  6. ↑ a b Weisstein, Eric W.: Midpoint Polygon (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
  7. ↑ Weisstein, Eric W.: Derived Polygon (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)